Jim Milner sculpture - Yorkshire - maths stone sculpture - Phi and Pi III

Contact Jim on 01226 763124 or milner44@btinternet.com
		Why and how?	News

Home

Geometric gallery

Maquettes

Fractal gallery

Maths gallery

Figurative gallery

Delivery and Installation

The J,N & J Equation - The Sums of Convergent Fractal-fractal Geometric Series. 2014. 130cm x 80cm. Engraved and painted sandstone. [not for sale]


This relationship was discovered and proved by three undergraduate friends – Jim Granger, Natalie Parazhang and myself – at Sheffield Hallam University in 2001 ¹. The equation describes the geometry of a more complex type of fractal than Sierpinski’s gasket – that of fractal-fractals. 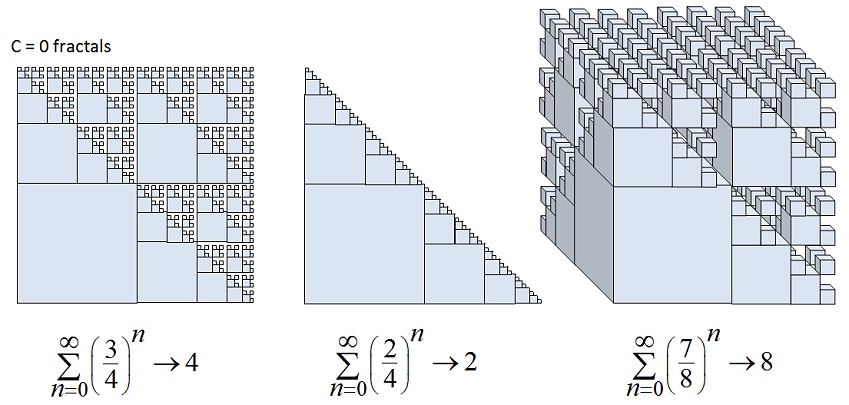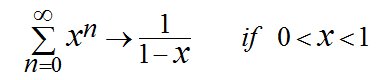In terms of this equation, Sierpinski’s gasket is a C = 0 type fractal, and its geometry is described by the equation for the sum of a simple convergent geometric series : An equation which turns out to be a special case of the J,N & J equation for when C = 0. 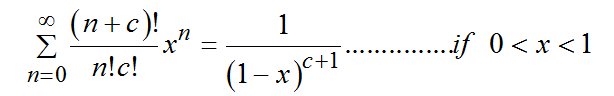The left- hand side of the equation describes the complex convergent geometric sums of fractional areas, and the right-hand side describes the limiting areas of the space filling fractals that the sums equate to. All of these series are convergent - the greater C or X are, the slower the series converges to its limit. If you are interested in finding out more about fractal-fractals, please read on .............................
Fractals, fractal-fractals, fractal-fractal-fractals and so on.
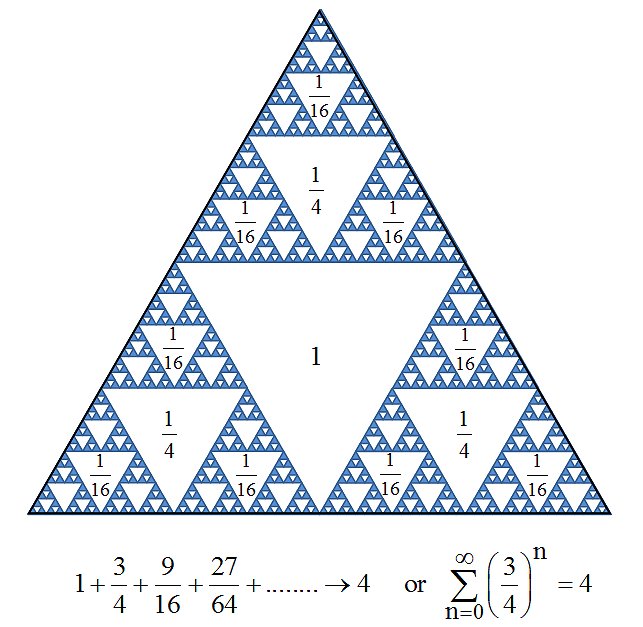Waclaw Sierpinski’s gasket, below, is famous for a number of complicated mathematical reasons, but let’s think about it now as a simple thing – as just a charming geometric demonstration of the sum of a simple infinite convergent geometric series – a proof without words. - since the area of the resulting fractal is four times the area of the largest triangle in the series. We can think about it as the addition of an infinite number of variously sized equilateral triangles to create a bigger equilateral triangle. Suppose we replaced all the variously sized little triangles with Sierpinski gaskets of the same size: 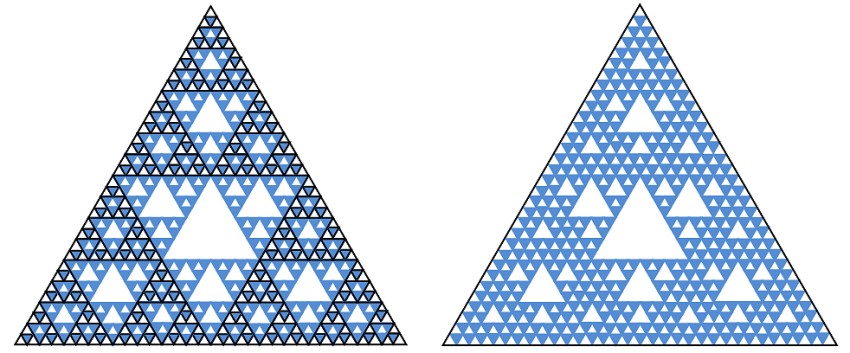The resulting ‘fractal-fractal’ is a geometric demonstration of the sum of a more complex convergent geometric series, 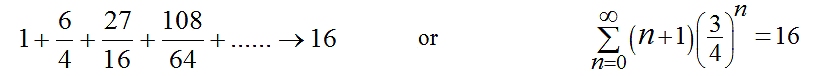- since the area of the resulting fractal-fractal is now 16 times the area of the largest triangle at its centre. Since a fractal can be used as the building block to construct a more complex fractal-fractal, the fractal-fractal can itself be used to construct a fractal-fractal-fractal, and so on ad infinitum; but what complex geometric series will they represent? – and would it be possible to generalise the results? 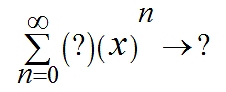Jim Granger, Natalie Parazhang and I got together to try to answer these questions while we were undergraduates in 2001.
	$Fractal fractal engraved sandstone$
Sierkinski’s Gasket, 2014, 42cm by 42cm.	Fractal-fractal, 2014, 42cm by 42cm.
The J, N & J Equation.
Instead of working on fractal-fractal versions of Sierpinski’s gasket, we used a square fractal version of the same series since it contained the possibilities of three different series which might help us to generalise our results:

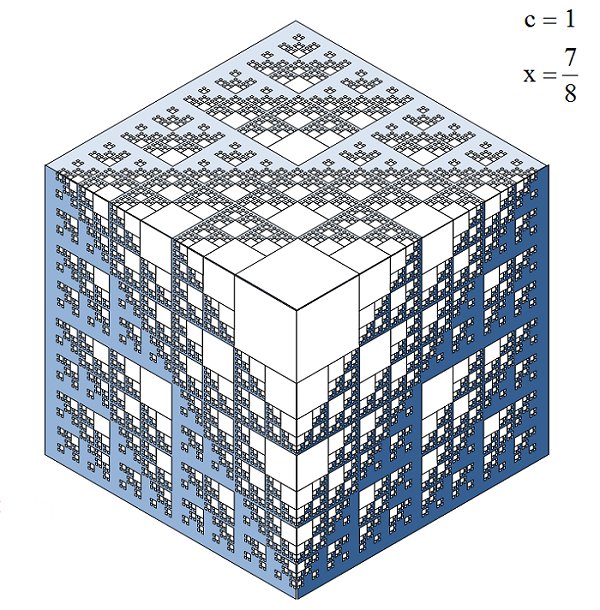
Fractal Cube. 2014. Engraved 8" fine grained sandstone cube.
Jim Granger used the computer program Logo to produce these images of C = 1, 2 & 4 fractal-fractals for us to analyse the geometric series involved:
fractal, F₀	fractal-fractal, F₁
	$Fractal fractal F1$
fractal-fractal-fractal, F₂	fractal-fractal-fractal-fractal, F₃
$Fractal fractal fractal F2$	$Fractal fractal fractal fractal F3$
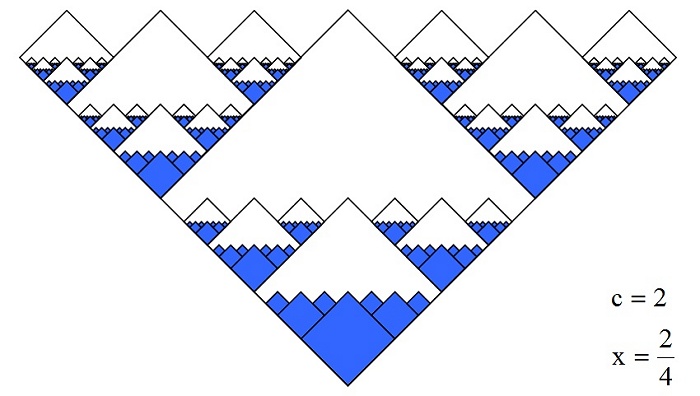
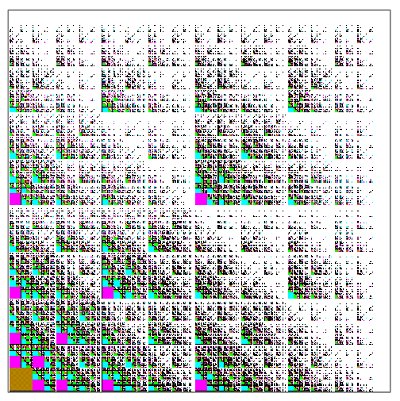
Jim colour-coded the different sized squares to make them easier to count to analyse the series. I was able to generalise the results by considering similar fractal-fractals where C = 1 & 2 and X = 2/4 & 7/8, as well as a certain amount of algebraic pattern spotting and guesswork. Here is a proof by induction of the JNJ equation: ¹ MILNER, J. PARAZHANG, N & GRANGER, J. 2001. Philosophy and Practice of Mathematics & Proof in the 20th & 21st Centuries. The Fractal-fractal and the JNJ Theorem. Unpublished paper. Sheffield Hallam University, UK.
The JNJ Equation & the Sums of Differentiated Geometric Series
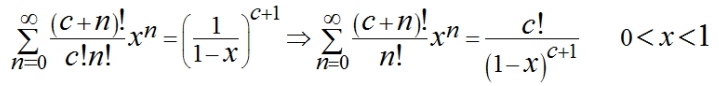The JNJ equation is also the sum of various numbers of different orders of differentiated geometric series, and so these series can be derived from the equation without the use of calculus. For example, if C = 1: 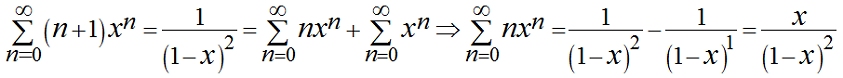if C = 2: 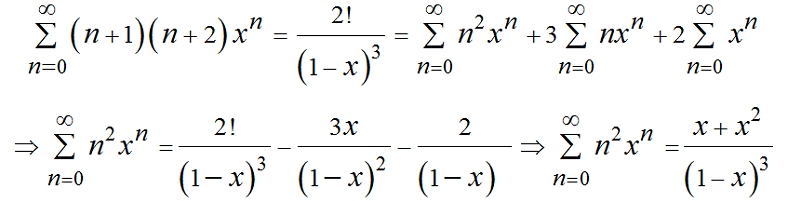And so, all the sums of differentiated geometric series can be derived algebraically from the JNJ equation 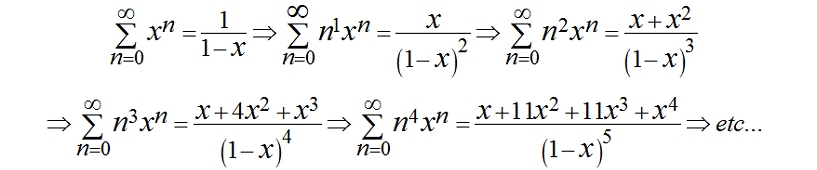However, the method of using calculus to find the sums of these series is less long-winded.
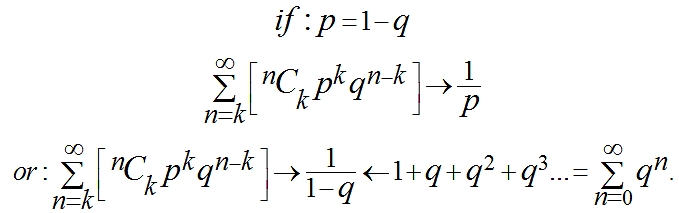The JNJ Equation & Probability
A probability equation can also be derived from the JNJ equation: Chance 2014. Engraved and painted fine-grained sandstone. 50 x 20 cm
Works in Progress? A fractal-fractal cube? $JNJ Fractal fractal cube$ Icebergs?