Elemental forms & Geometric sculpture

Snowdrifts & other elemental forms

In March 2013, we had a foot of snow here on the eastern upland approaches of the Pennines. The higher fields were almost swept clear of the snow by the strong east wind and the snow drifted to up to eight foot high beside the dry-stone walls and in the lanes.

My friend Elizabeth, who was cut off by the drifts in these fields and lanes, emailed me that while struggling to look after her nine sheep and twenty hens, she had been delighting in the beauty of the drifts. She wrote 'Whenever I look at their shapes and ridges, they remind me of your sculptures. There is a similar delicate precision to the ridges of the snowdrifts and to the changing forms beneath them.’

The drifts were less dramatic down in the valley where I live, but through my kitchen window I could see an unusual drift, which jutted out from the roof of the workshop and the top of the garden wall. I took pictures of it over the course of a few days, and saw how the form of it gradually changed – caused by partially thawing in the middle of the day and then refreezing at night:

The elemental forces which create snowdrifts, sand-dunes and shape our landscape are different to the ways we use to construct our built environment - where we construct mainly flat surfaces, constant angles between surfaces, and an emphasis mainly on horizontal and vertical surfaces.

Some modern geometric sculpture and graphic art build on the forms and structures we habitually use in our built environment. Iterative processes can be used in fractal structures to produce images of infinity to alleviate the monotony of this. Random elements can also be entered into computer programs to simulate how our natural world has been, and is being, formed - but perhaps these engage us less on a visceral level than the strange works of nature.

The elements use a different logic to form our natural world. Certainly, there is randomness behind elemental forms, but there is causality there as well:

So how could a geometric sculptor attempt to of recreate such forms?

For the last three years, I have been experimenting with geometric sculpture to try to mimic natural elemental forms shaped by the action of wind and water and frost. The sculptures’ surfaces are warped rather than flat, and the angles between surfaces gradually vary. I hoped that by these means I could to turn the stone I was carving from an inert form into something almost dynamic and sensual – not a natural organic form, but an elemental form.

And yet, the works have been designed using only Euclidean geometry:

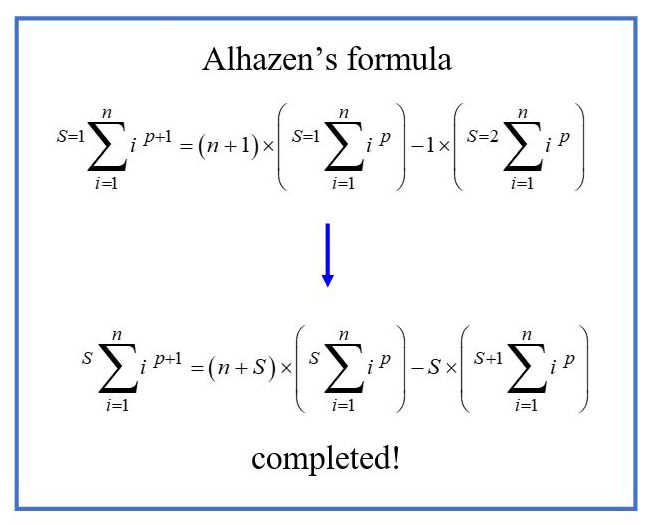
Here is a maths bit about how I have gone about it:

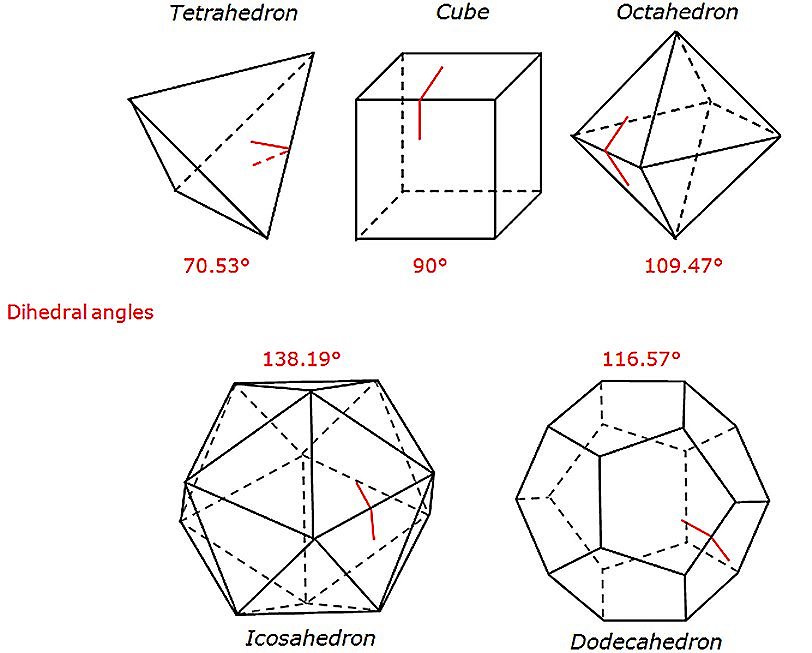
Dihedral angles

The greatest angle that two surfaces make with each other is called their dihedral angle. The dihedral angles of the Platonic solids for example are shown below:

Unsurprisingly, the dihedral angle most commonly used in our built environment is 90° - a right angle.

My first experiment in using varying dihedral angles in a geometric sculpture was in the design of a little water feature:

The cross-section of the central piece varies from a rectangle at the bottom to a perfect diamond at the top. The dihedral angle of two of the edges vary between 90° and 120° and the angles between the other two sides vary between 90° and 60°, warping each of the upright surfaces.

I used a similar design for an eight foot twisted obelisk. The obelisk is an exploration of some simple but strange transformations of geometric forms. Viewed from the side, it appears to have three perfectly straight edges. As one moves around the sculpture, two of these edges gradually transform into sinuous curves while the third remains straight. As one moves further around to the front, one curve is lost to view, to be replaced on the other side with a straight edge. The cross-section of the base of the obelisk is a near perfect golden-section rectangle which twists anti-clockwise and transforms into a perfect diamond at the top.

Click on the video of a small model being rotated, to see these transformations:

In the next series of sculptures, I tried using these techniques with circular and egg shaped sculptures rather than obelisks – creating Möbius solids.

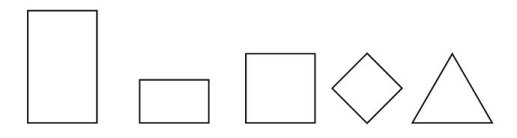
The torus cross-sections I have most often used for these sculptures have been golden section rectangles, squares and an equilateral triangle:

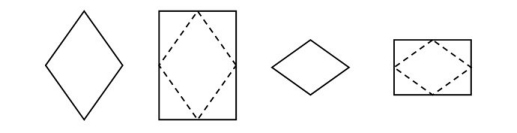
- combined with perfect diamonds and the rectangles which contain them:

Mobius Strips and Solids

Here is how to make a Möbius strip: - take a strip of paper - twist one end of it through 180° - turn it round into a torus and then overlap and stick the two ends together with glue:

Were you to draw a pencil line down the middle of the strip, you would find that the line covered both sides of the paper and then joined back to its starting point. Similarly, if you were to trace an edge, you would find that the strip had only one edge – not two.

Asymmetry

Möbius sculptures which have a base of one cross-section which warps and transforms to another cross-section at the top are always identical when viewed from the front and the back, if the initial torus shape has a vertical plane of symmetry.

If, however, the initial torus doesn’t have a vertical plane of symmetry, such as an egg shape on its side, the same warping from top to bottom results in sculptures which have very different forms when view from the back and the front. Here is an example of two sides of such a sculpture:

Here are some other examples of this type of sculpture:

The torus of the circular sculpture below doesn’t have symmetry in a vertical plane because the centre of the inner cut-out circle is not on the vertical diameter of the outer circle.

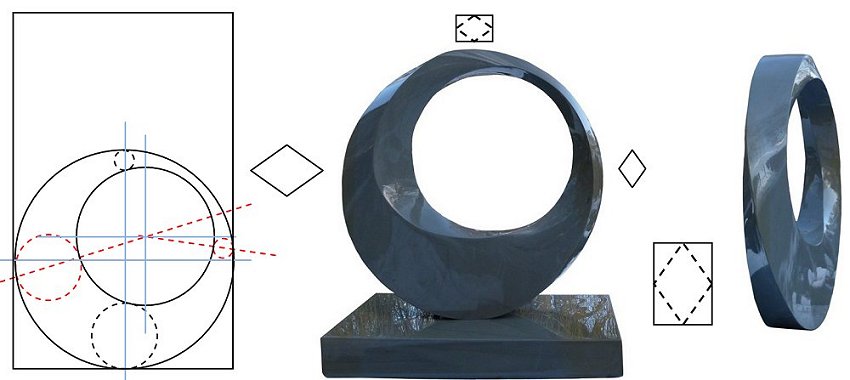
Here are front and back views:

By mirroring the right-hand picture below, we can see that the back and front are not even mirror images of each other, but distinctly different sculptural forms:

I’m pleased with this sculpture and have nicknamed it Ich habe genug – I have enough – homage to the great genius J S Bach.

A recent commission was for a very small Möbius for a lady in New Zealand. In our emails we just referred to it as the little blue Möbius. The thought now occurs to me that I should have named it Tangled up in Blue, as a tribute to another great genius, Bob Dylan?

I’ve enjoyed my three years experimenting with geometric sculpture to try to re-create elemental forms - designing four large obelisks and about twenty large Möbius sculptures. I’m getting old now – perhaps I have made enough large sculptures? I think I’ll spend some of my dotage making little ones – I liked Tangled up in Blue and miss having it on my kitchen windowsill.

Jim Milner, 2015